Kalman Filter Explained Simply

The truth is, anybody can understand the Kalman Filter if it is explained in small digestible chunks. This post simply explains the Kalman Filter and how it works to estimate the state of a system.

The big picture of the Kalman Filter

Lets look at the Kalman Filter as a black box. The Kalman Filter has inputs and outputs. The inputs are noisy and sometimes inaccurate measurements. The outputs are less noisy and sometimes more accurate estimates. The estimates can be system state parameters that were not measured or observed. This last sentence describes the super power of the Kalman Filter. Again, the Kalman Filter estimates system parameters that are not observed or measured.

In short, you can think of the Kalman Filter as an algorithm that can estimate observable and unobservable parameters with great accuracy in real-time. Estimates with high accuracy are used to make precise predictions and decisions. For these reasons, Kalman Filters are used in robotics and real-time systems that need reliable information.

What is the Kalman Filter?

Simply put, the Kalman Filter is a generic algorithm that is used to estimate system parameters. It can use inaccurate or noisy measurements to estimate the state of that variable or another unobservable variable with greater accuracy. For example, Kalman Filtering is used to do the following:

• Object Tracking – Use the measured position of an object to more accurately estimate the position and velocity of that object.
• Body Weight Estimate on Digital Scale – Use the measured pressure on a surface to estimate the weight of object on that surface.
• Guidance, Navigation, and Control – Use Inertial Measurement Unit (IMU) sensors to estimate an objects location, velocity, and acceleration; and use those estimates to control the objects next moves.

The real power of the Kalman Filter is not smoothing measurements. It is the ability to estimate system parameters that can not be measured or observed with accuracy. Estimates with improved accuracy in systems that operate in real time, allow systems greater control and thus more capabilities.

Kalman Filter Algorithm Overview

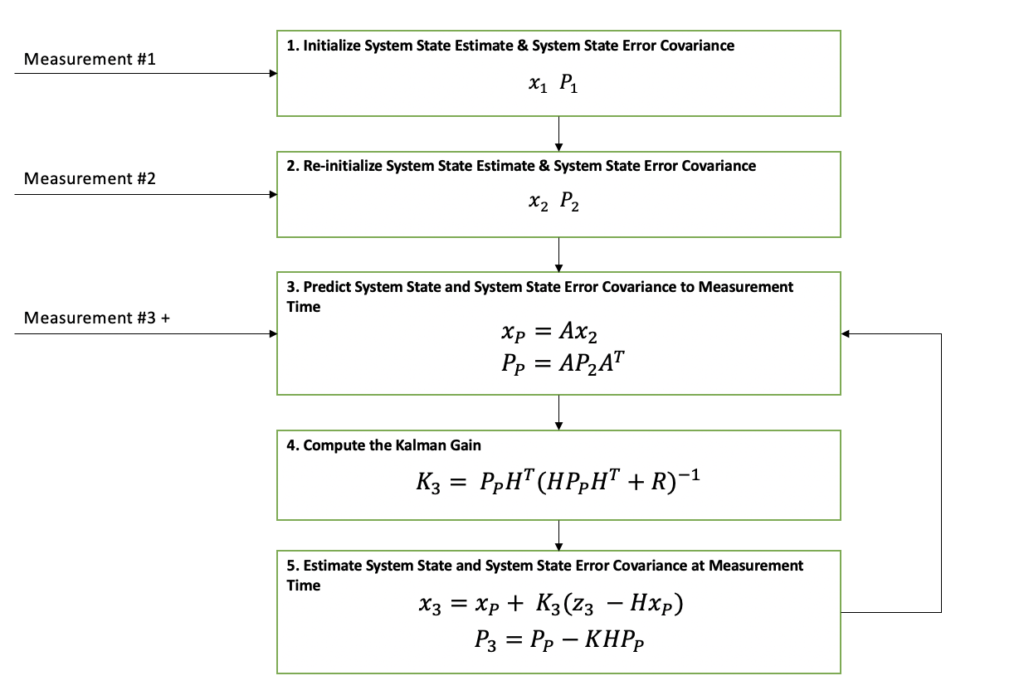
The process diagram above shows the Kalman Filter algorithm step by step. I know those equations are intimidating but I assure you this will all make sense by the time you finish reading this article. Let’s look at this process one step at a time. For your reference, here is a table of definitions that will be referred to throughout.

x	state variable	n x 1 column vector	Output
P	state covariance matrix	n x n matrix	Output
z	measurement	m x 1 column vector	Input
A	state transition matrix	n x n matrix	System Model
H	state-to-measurement matrix	m x n matrix	System Model
R	measurement covariance matrix	m x m matrix	Input
Q	process noise covariance matrix	n x n matrix	System Model
K	Kalman Gain	n x m	Internal

The table above identifies the variables used in the algorithm. Each variable listed has a structure type and category. As this article continues, use the table as a reference.

---

If you are enjoying this post, check out my book Kalman Filter Made Easy. You will learn: the first principles behind the Kalman Filter, how to create simulations and perform analysis on Kalman Filters, and more.

---

Kalman Filter Radar Tracking Tutorial

This tutorial will go through the step by step process of a Kalman Filter being used to track airplanes and objects near airports. The output track states are used to display to the air traffic control operators monitoring the air space.

Kalman Filter Tutorial Notation

Radars are not built equally. Each one has different capabilities and therefore provides different types of information to its supporting systems. For this example, the radar will output its measurements in 2D cartesian coordinates, x and y. These measurements will be represented as a 2-by-1 column vector, z. The associated variance-covariance matrix for these measurements, R, will also be provided by the radar along with the time tag for when the measurement occurred, t. The subscript m denotes the measurement parameters. And the k subscript denotes the order of the measurement.

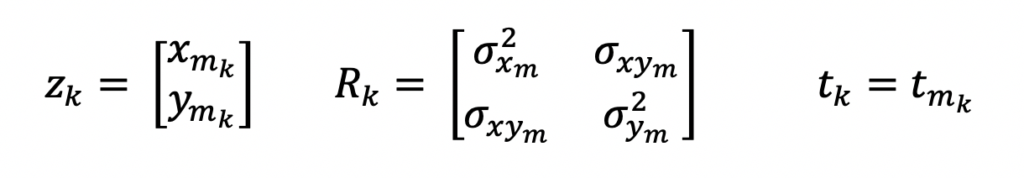
The Kalman Filter estimates the objects position and velocity based on the radar measurements. The estimate is represented by a 4-by-1 column vector, x. It’s associated variance-covariance matrix for the estimate is represented by a 4-by-4 matrix, P. Additionally, the state estimate has a time tag denoted as T.

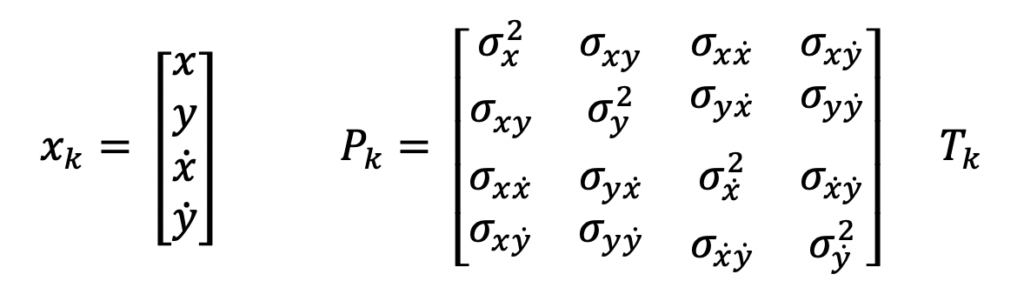
Step 1: Initialize System State

Initializing the system state of a Kalman Filter varies across applications. In this tutorial, the Kalman Filter initializes the system state with the first measurement.

xk	Eqn. 1-1
Pk	Eqn. 1-2

In this radar tracking example, the input measurements contain position only information. The output system state will contain the position and velocity of the object.

When the first measurement comes, the only information known about the object is the position at that point in time. The system state estimate will be set to the input position after the first estimate. The system state error covariance will be set to the first measurement’s position accuracy.

Initialize System State in Equations

These equations show the input and output values for this Kalman Filter after receiving the first measurement.

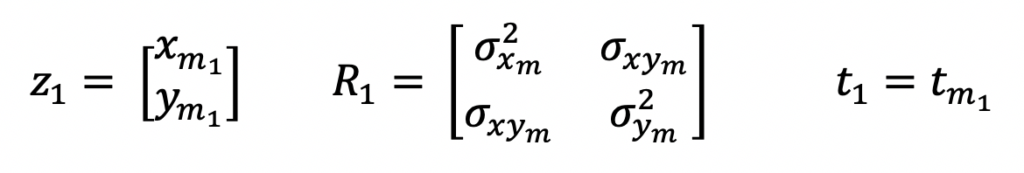
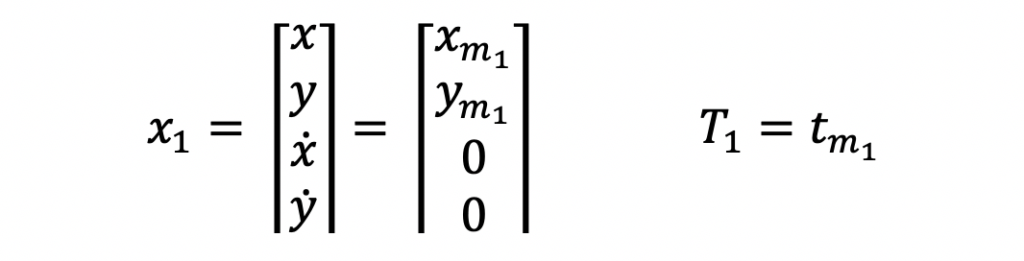
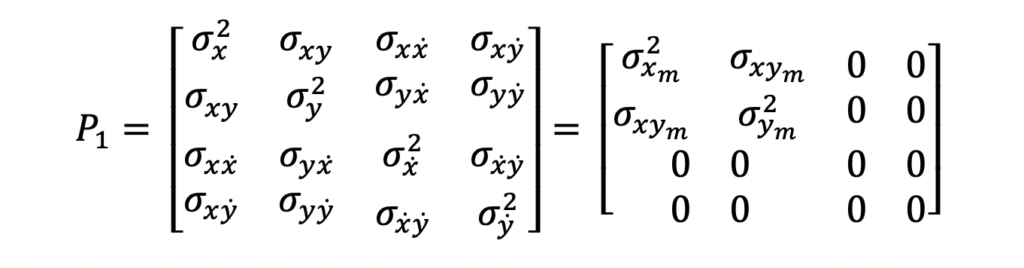
Step 2: Reinitialize System State

The system state estimate is reinitialized because a velocity estimate needs a second position measurement for computation.

xk	Eqn. 2-1
Pk	Eqn. 2-2

Velocity is estimated with a linear approximation. As you most likely recall from high school physics, velocity is equal to the distance traveled divided by the time it took to travel that distance.

The updated system state estimate will be the second measurement’s position and the computed velocity. The updated system state error covariance will be the second measurement’s position accuracy and an approximated velocity accuracy. Note that this velocity accuracy approximation is something that can be tuned and adjusted after running data through your filter. There are different ways of approximating these values so if this doesn’t match your approximation, that’s okay!

Reinitialize System State in Equations for the Kalman Filter

These equations show the input and output values for this Kalman Filter after receiving the second measurement. Note the velocity variance terms in the state covariance matrix. These values are being set to 10⁴. In other words, this value indicates a large uncertainty for the velocity state values. In this example, the velocity units are meters per second.

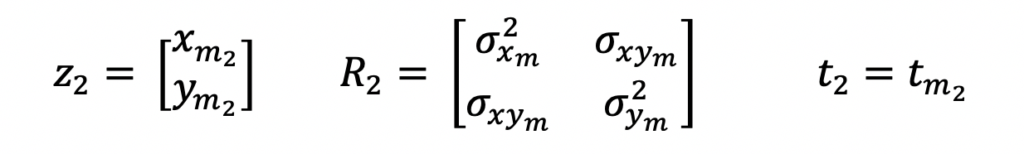
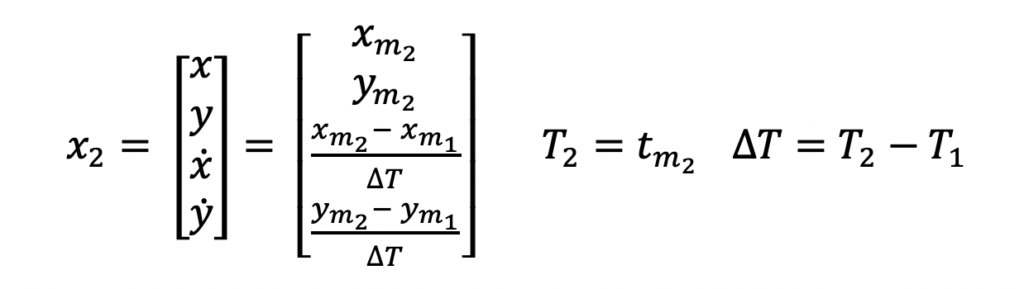
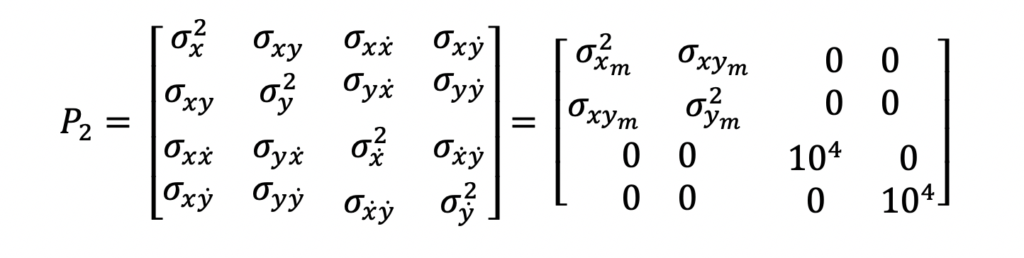
Quick Note on Initialization

Steps 1 and 2 used the first couple measurements to initialize and re-initialize the system estimate. Each application of the Kalman Filter may do this differently but the goal is to have a system state estimate that can be updated for future measurement with the Kalman Filter equations.

Steps 3 through 6 demonstrate how measurements are filtered in and the state estimate is updated.

Step 3: Predict System State Estimate

When the third measurement is received, the system state estimate is propagated forward to time align it with the measurement. This alignment is done so that the measurement and state estimate can be combined.

xp = Axk-1	Eqn. 3-1
Pp = APk-1AT + Q	Eqn. 3-2

The system model is used to perform this prediction. In this example, a constant velocity linear motion model is used to approximate the objects position change over a time interval. Note that a constant velocity model does assume zero acceleration. Remember this because it will resurface later.

The constant velocity linear motion model is something you may also remember from your high school physics class. The equation states that the position of an object is equal to its initial position plus its displacement over a specified time period assuming a constant velocity.

A state transition matrix represents these equations. This matrix is used to propagate the state estimate and state error covariance matrix appropriately. You may be wondering why the state error covariance matrix is propagated. The reason for this is because when a state estimate is propagated in time, the uncertainty about its state at this future time step is inherently uncertain, so the error covariance grows.

On the Q Matrix

The Q matrix represents process noise for the system model. The system model is an approximation. Throughout the life of a system state, that system model fluctuates in its accuracy. Therefore, the Q matrix is used to represent this uncertainty and adds to the existing noise on the state. For this example, the systems actual accelerations and decelerations contribute to this error.

On the H Matrix

The Kalman Filter uses the state-to-measurement matrix, H, to convert the system state estimate from the state space to the measurement space. For some applications, this is a matrix of zeros and ones. For other applications that use the Extended Kalman Filter, the H matrix is populated with differential equations. To learn more about Extended Kalman Filters, check out my article on them here.

In this tutorial, the H matrix is a simple matrix that is set up to reduce the state estimate and error covariance to position only values rather than position and velocity.

Predict System State in Equations

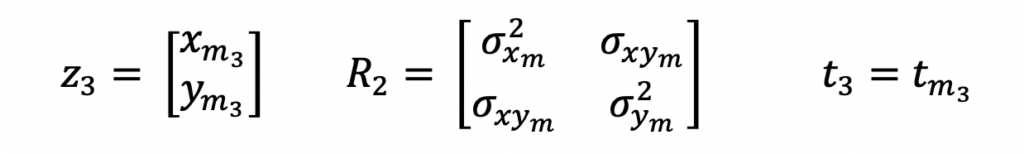
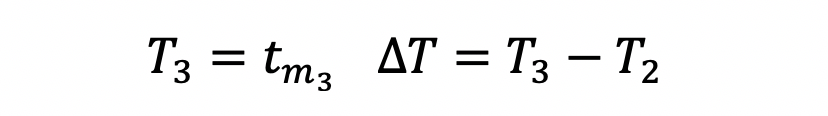
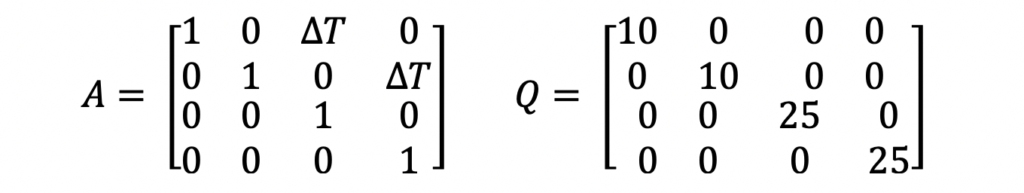
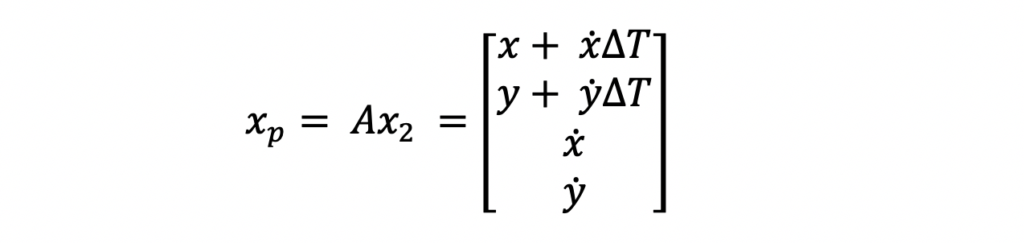
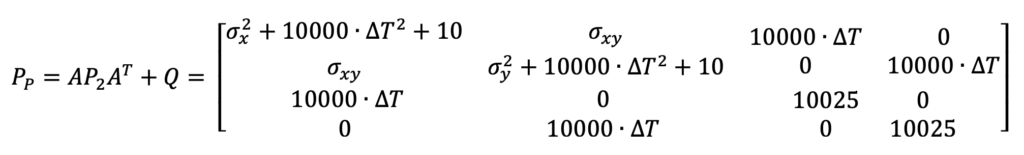
Step 4: Compute the Kalman Gain

This concept is the root of the Kalman Filter algorithm and why it works. It can recognize how to properly weight its current estimate and the new measurement information to form an optimal estimate.

K = PPHT (HPPHT + R)-1

Eqn. 4-1

Step 5: Estimate System State and System State Error Covariance Matrix

The Kalman Filter uses the Kalman Gain to estimate the system state and error covariance matrix for the time of the input measurement. After the Kalman Gain is computed, it is used to weight the measurement appropriately in two computations.

The first computation is the new system state estimate. The second computation is the system state error covariance.

xk = xp + K(zk – Hxp)	Eqn. 5-1
Pk = PP – KHPP	Eqn. 5-2

The state estimate computed above is the only state history the Kalman Filter retains. As a result, Kalman Filters can be implemented on machines with low memory restrictions.

---

If you enjoyed reading this post, check out my eBook Kalman Filter Made Easy and my Unscented Kalman Filter book. You will learn: the first principles behind the Kalman Filter, how to create simulations and perform analysis on Kalman Filters, how the Extended Kalman Filter and Unscented Kalman Filter work, and more!

---

Next Steps

I hope this post allowed you to see how amazing the Kalman Filter is. And when it is broken up into parts, it is not that intimidating.

In conclusion, the Kalman Filter is a generic process for optimal state estimation. It is used in a variety of applications that require accurate estimation. So now that you know what it is and how it works, go out and use it in your projects!

If you enjoyed reading this post, please share it with your friends on your favorite social network! Thanks for reading!